CoronadoSEAL wrote:
exactly what i was saying.
SenorToeNails, refute the last few posts please.
You're thinking about it the wrong way, IMO.
You think there is an infinitesimal (<-- an infinitely small number), other people have argued for their existence, but they just don't exist. And there is no real rigorous proof for them either + they are axiom dependent. Meaning they are definition dependent; unless & until you assume they exist and then rationalize their existence they don't exist. So why conjure such nonsense up?
You more or less thought of a number 0.00001 in your mind & that some where there's a small difference. But this is utterly wrong. You're not thinking of a number, that is your error. You should try and think of a logical representation for an idea instead.
Write it like this instead 0.000...01, what does the ellipses represent in this case; it represents infinity. So what is the value of the 01 part after infinity; an infinite expansion. As the expansion gets larger the value approaches zero. As an infinite expansion :: it equals absolutely nothing. It is zero.
0.00000...0 = 0.00000...01, seems strange at first but it isn't. And 0.999... = 1.
0.0...01
0.00...01
0.000...01
0.0000...01
0.00000...01 (it is getting smaller upon expansion, at infinity it equals zero) = 0
It is an infinite expansion that certainly resolves at being equal to zero. The ...01 part is non-existent, as the expansion is resolved at infinity. It is nearly the same idea as a limit in calculus.
0.9 + 0.09 + 0.009 + 0.0009 + 0.00009 + 0.000009... is just an algebraic expansion of the number 1 (with the ellipses representing the infinite expansion, and the Summation symbol not being shown).
0.9999... is just a condensed version of the algebraic expansion of the number 1. The sum resolves as the expansion approaches infinity to be exactly equal to 1.
Last edited by topal63 (2008-02-08 22:59:56)
 which is equivalent to 1.
which is equivalent to 1.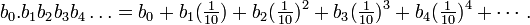
 lol
lol